The field of mathematics and statistics is frequently seen as a realm of precise, indisputable truths. Yet, every so often, a problem arises that not only challenges our understanding but also delights and mystifies us. One such enigma is the Monty Hall problem, a probability puzzle that has captivated and confounded thousands, including those armed with the mightiest weapon of academia – a Ph.D. The story of the Monty Hall problem is not just a tale of numbers and probabilities; it is a narrative that weaves through the human psyche, revealing our vulnerabilities and the limits of our intuition.
Monty Hall and the Conflicting Intuition
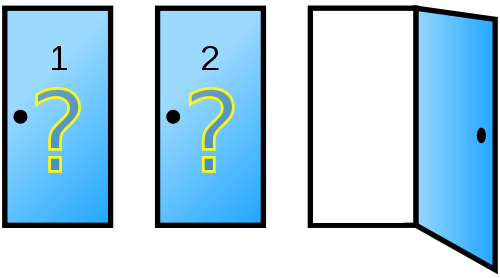
As beguiling as it may sound, the Monty Hall problem finds its roots in a simple game show scenario, where a contestant is faced with three doors. Behind one door lies a coveted prize, while the remaining two conceal nothing but goats. The contestant makes an initial choice, but before the reveal, a twist in the tale occurs. The host, armed with the knowledge of what lies behind each door, opens one of the unchosen doors to reveal a goat. The contestant is then given a choice: stick with the initial pick or switch to the other unchosen door. Intuition might lead one to believe that at this point, the odds are even – a 50/50 chance. However, the reality is counterintuitive; switching doors doubles the chances of winning the prize.
The uproar that followed Marilyn vos Savant’s exposition of the correct solution in her Parade magazine column is a testament to the problem’s puzzling nature. The sheer volume of dissent, especially from the academically adorned, underscores the innate conflict between our intuition and statistical reality. It is akin to the incredulity one faces when confronted with an optical illusion. Despite knowing the trick, the eyes (or in this case, the mind) refuse to concede. This phenomenon, where a clear statistical advantage is dismissed by the majority, highlights a fascinating aspect of human cognition and its occasional dissonance with mathematical truth.
In dissecting the Monty Hall problem, it becomes evident that the crux of the misunderstanding lies in our approach to probability. The common mistake is to view the final choice as an independent, random event, akin to flipping a coin. However, the situation is far from it. The initial choice has a one-third chance of being correct, leaving a two-thirds probability that the prize lies behind one of the other two doors. The host’s intervention, far from randomizing the outcome, actually skews the probability in favor of the door left unopened. This crucial insight reveals that the Monty Hall problem is not just a puzzle about probability, but also about how we process information and make decisions in the face of uncertainty.
The Math of Monty Hall: Solving the Paradox
The mathematical journey to unravel the Monty Hall problem is as captivating as the puzzle itself. Diving into the depth of probability and decision-making, this section aims to elucidate the underlying mathematical principles that render the Monty Hall problem a paradox of the veridical type – counterintuitive yet irrefutably true. The essence of solving the Monty Hall problem lies in our understanding of probability and the strategic maneuver based on information asymmetry between the contestant and the host.
At the heart of the Monty Hall problem is the principle of conditional probability, which fundamentally alters the landscape of decision-making from a simple random choice to a well-informed strategic move. Conditional probability, in this context, is the probability of winning the car given that the host has revealed a goat behind one of the unchosen doors. This pivotal moment in the game show scenario is where most contestants’ intuition fails them, leading to the widespread disbelief in the counterintuitive, yet correct, strategy of switching doors.
The mathematical exploration begins with a simple enumeration of possibilities, a technique often underestimated for its power in revealing intricate truths in probability puzzles. By assessing all potential outcomes, it becomes evident that switching doors indeed doubles the chance of winning. This enumeration underpins the fundamental principle of probability that the likelihood of an event is the ratio of favorable outcomes to the total possible outcomes. In the Monty Hall problem, the act of the host revealing a goat constrains the total possible outcomes in a way that favors the strategy of switching.

Delving deeper, the Monty Hall problem exposes the distinction between independent and dependent events. Our intuition errs by treating the final choice between the two doors as independent random events, akin to flipping a coin. However, the host’s intervention—knowing the location of the prize and deliberately choosing a door to open—introduces a dependency that skews the probability. This nuance is crucial for understanding why the probabilities are not equally split between the two remaining doors, but rather, the unchosen door inherits the combined probability of the initial wrong choices.
The problem illuminates the concept of information value in decision-making. Initially, the contestant’s choice among the three doors is purely random, with a one-third chance of selecting the prize door. The host’s action of revealing a goat behind one of the unchosen doors adds critical information to the scenario, transforming the seemingly random choice into an informed decision. This added information is what makes switching a statistically superior strategy, showcasing the profound impact of information on the probabilities of future events.
In essence, the Monty Hall problem is not merely a puzzle about choosing doors but a profound lesson in statistical reasoning, decision-making under uncertainty, and the critical evaluation of assumptions. The controversy and widespread disbelief that followed Marilyn vos Savant’s solution underscore the human inclination towards intuitive reasoning, often at the expense of statistical logic. The Monty Hall problem serves as a stark reminder of the limitations of intuition in the face of mathematical evidence and the importance of embracing counterintuitive truths in the pursuit of understanding complex phenomena.
The Monty Hall problem showcases the beauty and complexity of mathematical reasoning. It challenges us to question our assumptions, embrace the counterintuitive, and appreciate the intricate dance between probability, information, and decision-making. As we journey through the realm of mathematics, let the Monty Hall problem be a beacon, illuminating the path towards a deeper and more nuanced understanding of the world around us.
Related posts:
The Monty Hall Problem: A Statistical Illusion
Monty Hall problem
Why You Should Always Switch: The Monty Hall Problem (Finally) Explained